Determinan Matriks

DETERMINAN MATRIKS

Pengertian Determinan

Dalam bidang aljabar linear, determinan adalah nilai yang dapat dihitung dari unsur suatu matriks persegi. Determinan matriks A ditulis dengan tanda det(A), det A atau |A|. Determinan dapat dianggap sebagai faktor penskalaan transformasi yang digambarkan oleh matriks.

Perhitungan Determinan

Determinan Ordo 2x2

Bentuk umum matriks 2x2 :

$\textrm{A} \; = \; \begin{bmatrix} a & b \\ c & d \end{bmatrix}$

Apabila matriksnya berbentuk 2x2, maka rumus untuk mencari determinan yaitu :

Contoh :

Hitunglah nilai determinan dari matriks ordo 2x2 berikut ini :

Jawab :

det(A) = (3.8)-(5.4) = 4

Determinan Ordo 3x3

Bentuk umum matriks 3x3 :

$\textrm{A} \; = \; \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}$

Apabila matriksnya berbentuk 3x3, maka rumus untuk mencari determinan yaitu dengan Aturan Sarrus. Berikut penjelasan aturan sarrus yaitu :

Contoh :

Hitunglah nilai determinan dari matriks ordo 3x3 berikut :

Jawab :

det(A) = (2.4.1) + (3.3.7) + (4.5.0) - (4.4.7) - (2.3.0) - (3.5.1)

= 8 + 63 + 0 - 112 - 0 - 15= -56

Menggunakan Metode Ekspansi Laplace

Minor

Diketahui sebuah matriks A dengan ordo 3 seperti berikut.

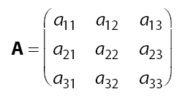
Matriks minor M_ijadalah matriks yang diperoleh dengan cara menghilangkan baris ke-i dan kolom ke-j dari matriks A sehingg diperoleh matriks minor berordo 2 seperti berikut.